
PocketCAS: Mathematics Toolkit (総合 4989位)
価格 : 3,000円
App Store 評価 :

4.7 (評価数 : 151)
カテゴリー | ソーシャルネット (アプリケーション) |
バージョン | 2024.1 |
App Store
更新日 | 2024/11/06 |
開発者 | Timing Software GmbH |
対応機種 | iPhone(iOS 12.0以降)、iPad(iPadOS 12.0以降)、iPod touch(iOS 12.0以降) |
対応言語 |  英語 ほか 英語 ほか |
サイズ | 34.7MB |
情報取得日 | 2024/11/23 |
| 
|
(評価数)
160
-
-
-
-
155
-
-
-
-
150
評価数(左、棒グラフ)、総合順位(右、折れ線グラフ)
151
151
151
151
151
151
151
151
151
151
151
151
151
151
151
151
151
151
151
151
11/14
11/15
11/16
11/17
11/18
11/19
11/20
11/21
11/22
11/23
(順位)
4.8K
-
-
-
-
4.9K
-
-
-
-
5K
|
※画像をクリックすると拡大します。






概要
PocketCAS はiPhone、 iPad、OS X対応の最も先進的な数学アプリケーションです。小学校から微積分、代数、統計までいかなる数学問題の解決も支援いたします。古いグラフ電卓を取り換え、宿題をお手伝いし、大学や業務上のいかなる計算も補助します。
このアプリは学生、教師、技術者にはなくてはならないツールです。大学レベルの微積分や代数を容易にするだけではなく、広範な範囲で活用できます。TI-89計算機と同等の機能を直感的で最新のインターフェースで提供します。すばらしいグラフ機能付きです。
無料のライト版
PocketCAS無料版 (PocketCAS ライト) によりPocketCAS プロの購入前に、インターフェースや多数の機能をご試用いただけます。以下に違いが説明されています。
数学能力
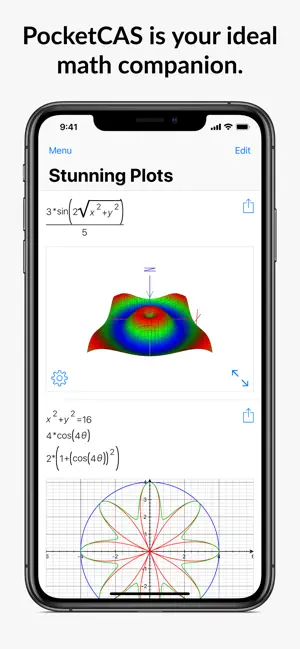
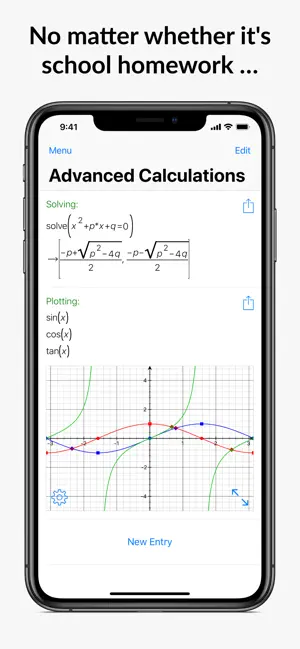
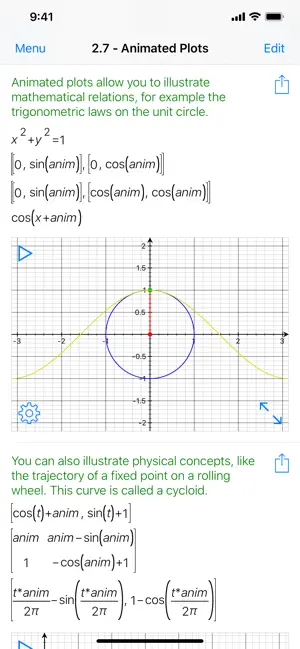
- 2Dプロット:すばやく2D デカルト、陰関数、極、パラメトリックプロットを作成。
- 3D プロット: PocketCASは驚愕的な3Dプロットを描写します!
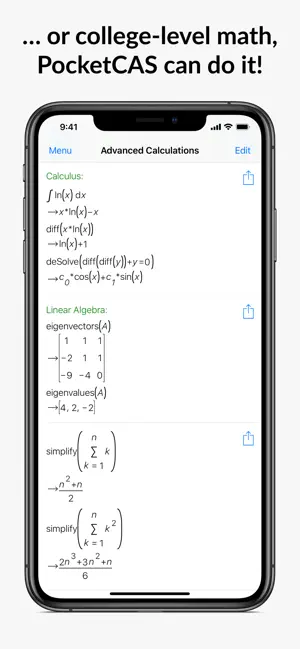
-微積分:極限値、導関数、積分、テイラー転換を計算。
- 線径代数: 行列の逆行列と積を求め、行列式、固定値の計算とその他を行います!
- 代数: 整数、多項式因数分解および除算を計算、置換、その他を使用。
- 解決: PocketCASはほとんどいかなる方程式も解きます。 線径方程式や常微分方程式までサポートします!
-スクリプト:PocketCASのCスタイルスクリプト言語はカスタム関数を定義し、条件式・ループを使用し、再帰をサポートします。
-物理単位:独創的な定数、単位を提供します。単位と共に方程式を入力すると、結果がお好みの単位に変換されます。
その他の機能
- エクスポート: プロット、入力、文書をPDFとしてエクスポートできます!
-数学キーボード:PocketCASの数学キーボードはApp Storeの中でも並ぶものはありません。
- ヘルプ: すべての機能は内蔵の参照に説明されています。行き詰ったら、多数あるチュートリアルやマニュアルをご覧ください(http://pocketcas.com/manual)。弊社のサポートにもお問い合わせいただけます(http://pocketcas.com/support)!
-オフライン計算:PocketCASは計算するためにインターネット接続を必要としません。
ライト版の制限
PocketCAS ライト版は以下のような制限があります:
- 多くの上級数学機能(例、積分、テイラー展開、固定値など)は利用できません。
- 1度に1関数だけプロットします。
- エクスポートしたグラフは透かし模様が入っています。
MAC 版
PocketCAS はOS Xでも使用できます。詳しい情報については、http://pocketcas.com/macをご覧ください。
レビュー
- 独学ツール 私は、現在70歳です、生涯学習のツールと
して、めちゃくちゃ便利いいです
自分で先にグラフを書き正解をたしかめるのに、使用させていただいております
また数学に独学を志ざす人のために便利な
ツールを考案して頂きます、事をお願いします。
- 便利 グラフのプロットや微分積分の計算など簡単な操作でできるので良い。最初のうちは操作に慣れないため少しもたつくが慣れるに従って入力も速くなってくるので便利さは一層増す。
- 流体力学を可視化して捉えられる 3Dアニメーションにて自身でイメージした波の形を簡易式で手軽にイメージの具現化ができるので重宝してます!!
多数項が周期波の形状にもたらすもの、乗数とは波の瞬間変化や ある系の相分布にどのような位置関係をもたらすか?(相対性理論) 項を括弧で閉空間の単項式で多数項の中に挿入したときの、系の中の固有相ができるもの(ウイルス→これが体内電位を狂わし悪影響を及ぼす等) 積分 微分 log e πの可視化などとにかく役に立っています!!!!!!
数学の式の意味や、なぜ天気予報での等圧線があのように描かれているのか?感覚的にアニメを作れるのでとにかくオススメです!!!!
一覧に戻る ※タイトルロゴをクリックしても戻れます。

